関数電卓の使い方 応用編
今回は少し応用的な関数電卓の使い方をいくつか紹介したいと思います
前回の記事を読んである程度使いこなせるようになっておけば今回の記事も読みやすいかと思うので是非そちらからどうぞ!
[blogcard url=“https://newskool-blog.com/2019/02/01/post-531/"]
今回使用する電卓はこちら
[itemlink post_id="1470″]
積分
問題を解くときに積分が出てくることってありますよね
そんなとき僕は今まで、一度式を積分してから関数電卓に値を打ち込んでいました
でもこれってめちゃくちゃ時間がかかるし、計算ミスも増えます
でもじつは関数電卓って式を打ち込めばそのまま値を求めてくれるんです!
では以下のかんたんな積分を関数電卓を使って解いてみましょう!
\[\int_{3}^{6} x^{2}+2x+1 \, dx \]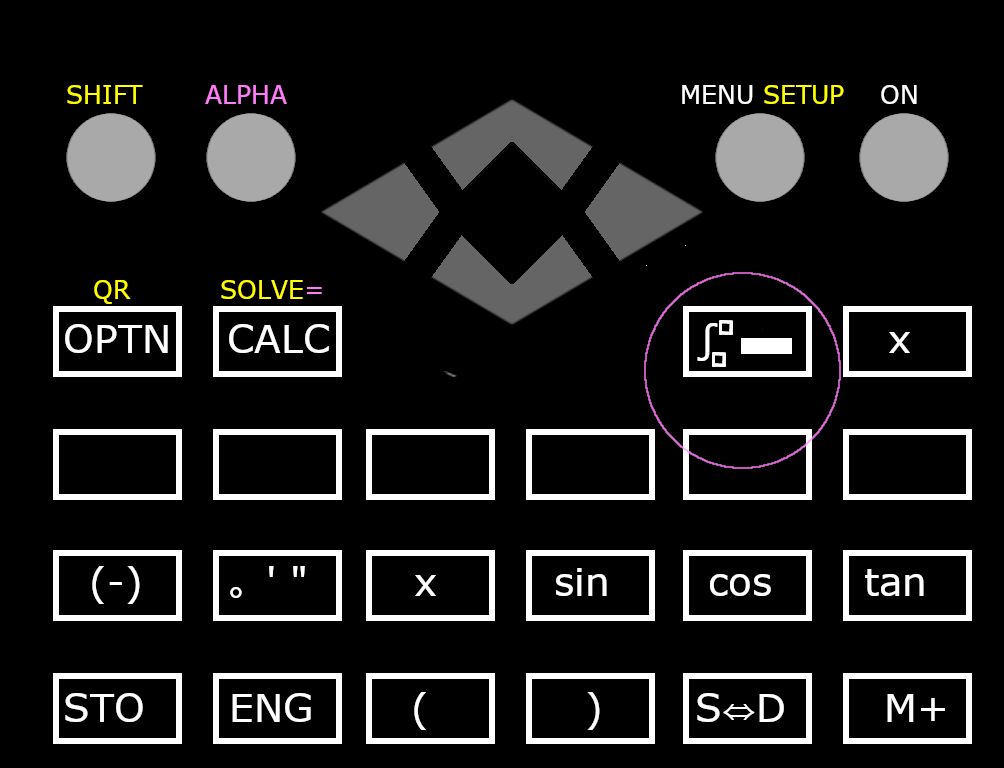
関数電卓のこのボタンを押すと積分記号が出てきますね
まずは積分したい式を代入しましょう

次に積分範囲を入力したら、あとは=を押すだけ!
とっても簡単に答えが出ましたね!計算ミスも減らせるのでぜひ覚えておいてください!
微分
積分もできるなら微分もできます
先ほどと同じ関数を使って微分係数を求めてみましょう
$f(x)=x^{2}+2x+1 (x=2)$
SHIFTを押して先程の積分マークを押すと以下のような画面になると思います(ボタンの上に黄色で微分のマークが表示されてますよね)
あとは微分したい式を打ち込んで$x=2$を入れれば結果が出てきますね
方程式の解
1次方程式の場合
1次方程式は基本計算から行うことができます
今回も簡単な式を例にしてみます
$X+2=11$
こんなの暗算でできると思いますがどんなに複雑な式でも変数が1つだけなら応用させることができるので覚えておいて損はないです
まず$X+2$を打ち込んだらALPHAを押してCALCを押してください
これで=が出ますよね
通常の=は押すと答えが表示されますが、この=は式中に表示できます
そのまま$9$を押して、今度はSHIFTを押してからCALCを押します
すると$X$の値が表示されます
2~4次の方程式
では次は2次の方程式で考えましょう
$x^{2}+5x+13=7$
という式の解を求めてみます
MENUからA:方程式/関数 計算
を選びます
2:高次方程式を選び、次数を選択します(今回は2)
このとき、式の形は
$ax^{2}+bx+c=0$
にしなければいけないので入力するときは
$1x^{2}+5x+6=0$と書き換えるか、計算が面倒な人は
$1x^{2}+5x+13-7=0$と入力してください

あとは=を押せば2つの解が表示されます!
連立方程式
次は連立方程式です
$2x+y=3$
$3x+5y=1$
MENUからA:方程式/関数 計算
1:連立方程式を選択し変数を選びます(今回は2)
あとは式に値を代入して=を押せば結果が出ます
まとめ
いかかがでしょうか?わかりにくいところや、こういう事ができるのかみたいなコメントもどしどし送っていただけるとありがたいです!
今回も読んでいただきありがとうございました!


