関数電卓の使い方 最小二乗法
前回は関数電卓の使い方基礎編を書いたけど、1年経って今まあまあ見られてるということを知ったので第二弾をやろうと思う。前回同様にベースとなる関数電卓はこれ
今回は最小二乗法のやり方を書くけど、まず最小二乗法ってなにそれ概念がわかりにくいし謎~理解できない~って人も多いと思うからまずは最小二乗法について解説していく。
最小二乗法とは
最小二乗法(さいしょうにじょうほう、さいしょうじじょうほう;最小自乗法とも書く、英: least squares method)は、測定で得られた数値の組を、適当なモデルから想定される1次関数、対数曲線など特定の関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差の二乗和を最小とするような係数を決定する方法、あるいはそのような方法によって近似を行うことである。
これを読んで理解できる人は理系科目のセンスがあると思う。素晴らしい。残念ながら大学2年の俺にはこの概念が全く理解できなかったし理解しなくても生きていけた。だから何も心配することはない。でも知っておいて損することもない。
だから具体例を上げてみる。以下に小学校の各学年における女子の身長と体重のデータを示した。
| 年齢(歳) | 身長(cm) | 体重(kg) |
|---|---|---|
| 7 | 122 | 23.3 |
| 8 | 126.7 | 24.7 |
| 9 | 134.2 | 29.8 |
| 10 | 138.3 | 31.7 |
| 11 | 148.1 | 39.4 |
| 12 | 149.5 | 41.8 |
これを身長を縦軸、体重を横軸にしてプロットするとこうなる。
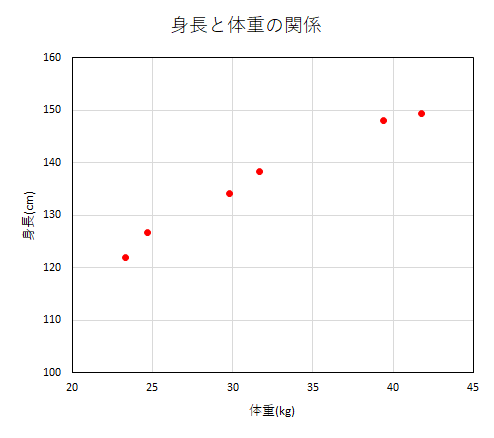
さて、この図を見ていると全部の点を通る直線は引けないけど、なんとなく全部の点に近い位置を通る直線が引けそうだなと思う。
じゃあ、もっとも全部の点に近い位置を通る直線ってどうやって引けばいいのか考えてみた。
まず求めたい直線をY=aX+bと仮定しよう(ここでXは身長、Yは体重とする)。
a,bは定数だから一定、YはXの値により変化する。ここまでは多分ついてこれると思う。
ここで7歳の体重を仮定した直線のYの値から引いてみる。つまりY-23、ここでYはaX+bと置いてるから、差は以下のように表しても何も問題はない。
$(差)=Y-23.3=a・122+b-23.3$
122はXつまり今回は7歳の身長の値のこと。
各点の値と求めたい直線の差は、直線の上に点があるのかそれとも下にあるのかによってプラスとマイナスになる。しかしプラスに4ずれていようがマイナスに4ずれていようが、求めたい直線からの距離は4。
そこで差の二乗を取ることで符号の差をなくし、差の二乗の合計値が最も小さくなる値をとる直線が求めたい直線ということになる(ここが理解しにくい気がする)
でもまあ二乗の値が最小になるから最小二乗法なんだ、名前そのまんまなんやなっていうのが分かってもらえたと思う。最もすべての点と直線の距離の二乗が近い直線ってことやね。
この計算、手でやるとものすごく面倒やからエクセルなんかでやると思うんやけど関数電卓でもできる。試験で最小二乗法が必要になるときにパソコンは持ち込めないから関数電卓で最小二乗法をやる機会は結構あるかもしれない。実際俺がそうだった。
以下にその手順を示していこうと思う。
関数電卓での最小二乗法のやり方
先程の身長体重を例に関数電卓で最小二乗法を行う
MENU→6:統計計算を選択(6を押す)

の中から自分が行いたい計算を選ぶ。今回は
2:$y=ax+b$
で行えばOK

このような画面になるのでx、yに値を代入していこう
データを打ち終わったらACを選択→OPTNを選択→回帰計算一覧を選択

この画面からa,bの値が読み取れる、意外と簡単。
よって先程例に示した身長と体重の関係は最小二乗法を用いると
$Y=1.46X+90.0$
という直線で近似できるということになる。
まとめ
以上が関数電卓を用いた最小二乗法の導出方法。 関数電卓に関する記事ももっと増やしていきたいと思っている。今回も最後まで読んでいただきありがとうございました。


